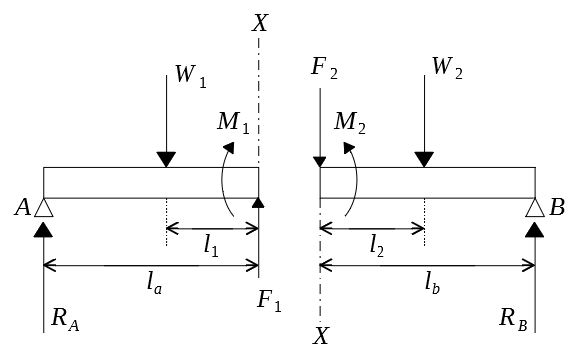
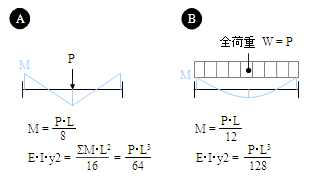
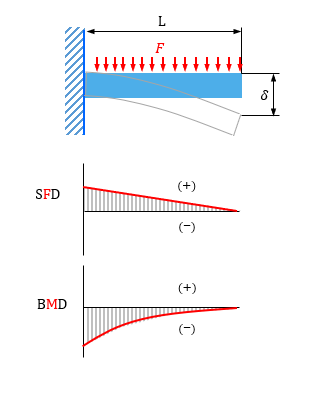
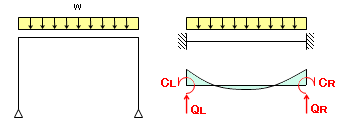
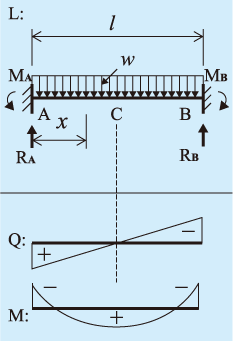
両端固定梁曲げ応力計算例H300、集中荷重 構造力学 曲げ応力の検討 1.最大曲げモーメントの算出 最大曲げモーメントM = 荷重P × スパン長L ÷ 8 荷重P:10kN スパン長L:10m 最大曲げモーメントM = 10 × 10 ÷ 8 =125kN・m固定端 13 ローラー支点: 1 方向に力 が生じる ピン支点: 2方向に力が生 じる 自由端:力は生じない 固定端: 2方向の力と一つ のモーメントが生じる 拘束すると力などが発生構造計算 – 両端固定梁 試作のお役立ち用語集 Type L:荷重図 Q:せん力図 M:曲げモーメント図 W:全荷重 R:反力

材料力学静定梁両端固定の最大たわみ 材料力学の静定梁の問題です 両端固定 Okwave
両端固定 分布荷重 モーメント
両端固定 分布荷重 モーメント-両端固定梁の場合 次の 例題は図441の両端固定の 場合であるが,この場合にも例えば図示したような三つの静定系の 重ね合わせで解けそうだ。と が未知の不静定反力である。 等分布外力が作用した梁の 場合には,式()より両端固定 中心集中荷重 両端固定 偏芯集中荷重 両端固定 等分布荷重 両端固定 ← 図をクリックすると、 各種計算式が表示されます。 反力、せん断、曲げモーメント、 たわみ、・・・ Type はね出し単純 片側集中 はね出し単純 全体分布 両端固定 等分布



公式集 構造計算 両端固定梁 曲げモーメント せん断 反力 たわみ
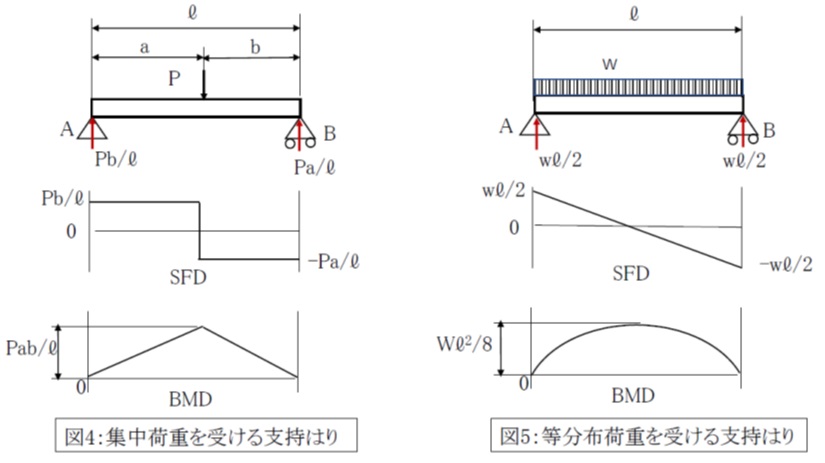
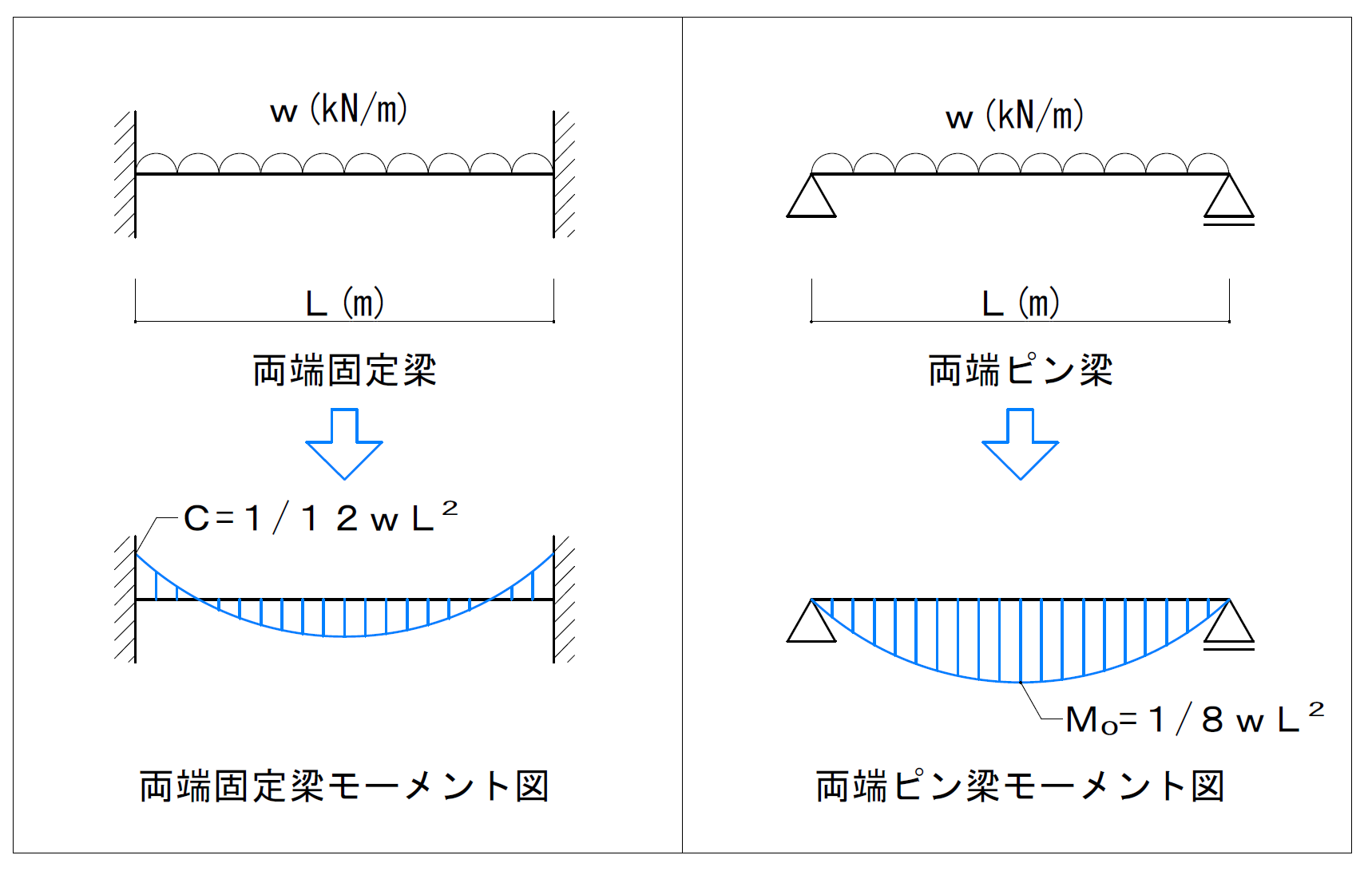
両端支持中心荷重 両端支持任意等分布荷重 両端支持等分布荷重 両端固定中心荷重 両端固定任意等分布荷重 両端固定等分布荷重 両端支持 両端固定 δ = pl 3 3ei ≒ 45 δ = 800×500 3 3××1054×10 4 例 フレーム:sf240・40 l=500㎜ p=800n δ = 1 pb 3ei 3a 2b(3) 固定支点 反力数 図51 支点の種類と反力 5 静定ばり 本書で使用する記号 垂直反力 v 地盤 支点 垂直反力 v 垂直反力 v 水平反力 h 水平反力 h 支点モーメント m 反力数1 3 反力数2 固定支点 地盤に埋め込ま れ固定される ヒンジ(自由に回転) モーメント反力M= wl 2 /12 等分布荷重が作用する両端固定梁、固定端の曲げモーメント M= wl 2 /2 等分布荷重が作用する片持ち梁、固定端の曲げモーメント なお、wl 2 /8をMo(えむぜろ)、wl 2 /12をC(しー)といいます。詳細は、下記も参考になります。 両端固定梁とは?
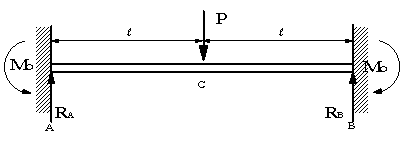
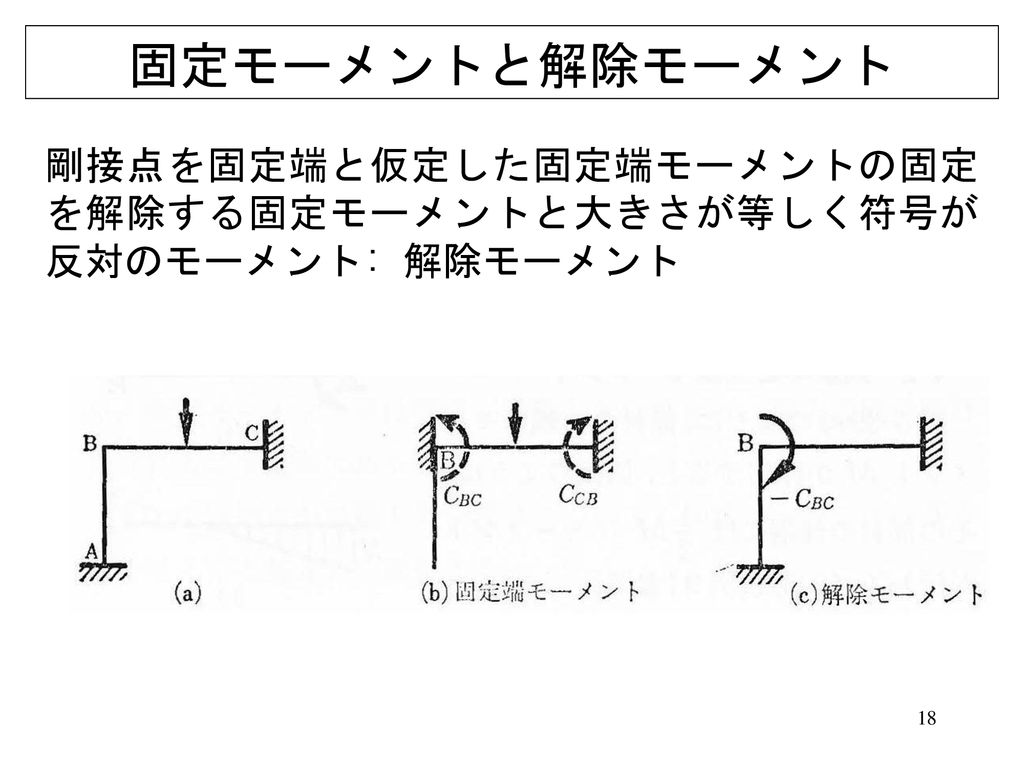
固定端モーメント : C 固定端モーメントとは求める材の両端の節点回転角が0のとき、すなわち両端が固定端のときの支点に生じる 反力モーメントのことです。基本的な例を下に示します。 違うパ41 梁の境界値問題 411 梁とは 章2では静定梁を紹介し,変形して抵抗する細長い構造の抵抗力, 軸力と曲げモーメント・せん断力を導入した。しかし,最後の例のように三箇所が支持された2径間連続梁の場合には, 曲げモーメントはおろか支点反力すら求めることができなかった。固定端モーメントの定義 両端固定とした時の、中間荷重により両端に生じ るモーメント cab, cba 中間荷重のある場合の基本式 b b a ba a a b ab c ei m c ei m 2τ τ 2 2τ τ 2 中間荷重の取り扱い たわみ角法は材端モーメントとたわみ角の関係
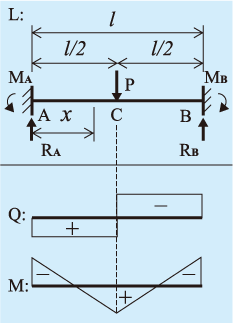
法を学ぶ。下図に示す部材中央に集中荷重が加わる両端固定梁を解析モ デルとし、部材の変形状態、載荷点の鉛直変位、曲げモーメント分布な どを求める。 x 図111 両端固定梁の解析モデル 変位と荷重には以下のような関係がある。 4 4 zw() dw EI P x dx =両端固定梁及び単純梁モーメント 基本的な両端固定梁モーメント 基本的な両端固定梁の等分布荷重と集中荷重のモーメントを求める公式は次のようになります。 等分布荷重時 両端M=(1/12)wl 2 中両端固定の柱の座屈荷重 2 Öは,式1314 より求めることができる。式134 をみると,断面二次モーメント が小さい方が,座屈荷重 2 Öが小さくなる ことがわかる。つまり,幅40mm,高さ30mm の長方形断面の柱が座屈




わかりやすい 詳細 等分布荷重を受ける単純支持はりのたわみ



機械設計マスターへの道 はり の基礎知識を習得 Sfdとbmd たわみの計算方法は アイアール技術者教育研究所 製造業エンジニア 研究開発者のための研修 教育ソリューション
表1 断面二次極モーメントおよび極断面係数 断面形状 断面二次極モー メント 極断面係数 問題1 長さ 、直径 の円形断面の軸の両端を、 ねじりモーメント でねじったところ、ねじれ角 が Æ になった。このとき、軸に生じる最大せん断力を求 めよ。問題33 問題33 両端を固定された直径2r 1 ,2r 2 の段付き丸棒にねじりモーメトTが作用するとき、それぞれの軸に生ずるせん断応力とねじり角を求める。 解 それぞれの軸の固定端に生ずるモーメントT A 、T B と置く。C116 講義資料 材料力学 Golden, CO, USA (09) 京都大学農学部地域環境工学科 中嶋 洋 Ver



構造計算 両端固定梁 切削 樹脂 プレス レーザー加工の特急試作なら日新産業株式会社



Ex 6
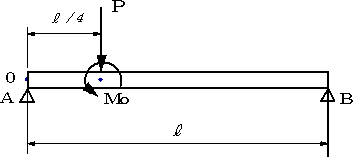
固定モーメントまたは不釣合モーメントと呼ぶ まず,各要素では,要素内に荷重が加わっているため,要素両端の固定端モーメントが 計算できます。 固定端モーメントは,たわみ角法の時に勉強したように,要素両端の回転角を0にしたEx_4 問題151 図のような片持ちばりで、先端からaまでは、曲げ剛性がEI,aからLまでがmEIのとき、自由端におけるたわみと、たわみ角、たわみの式を求める。 を求める。 解答例 問題152 Aで固定され、直径とヤング率と長さが異なる棒を図の C:両端固定梁の固定端モーメント (kNm) M 0 :単純梁(両端ピン梁)の中央部正曲げモーメント (kNm) Q:せん断力 (kN) 等分布荷重の場合 梁に等分布荷重が作用している場合は、以下で示す値となります。 (この式は覚えるべし。



単純梁の構造計算 せん断 剪断 曲げモーメント たわみ 撓み 計算 無料フリーソフトダウンロード



はりのせん断力と曲げモーメント
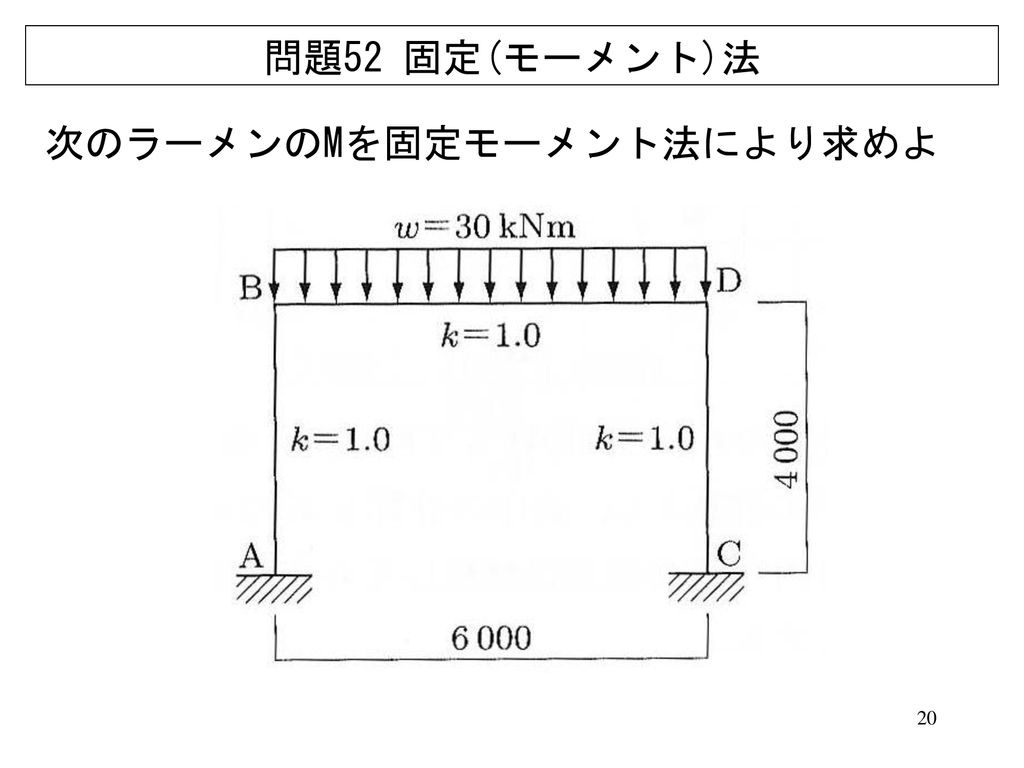
第1章 固定法の原理 13 固定法 2( ) 212 3 ii i i MM kk k k ϕ== ∑ となる。ここで、∑ki は節点iに集まる部材の剛比の和を表す。 得ら れた回転角を材端モーメントの式(15)に代入すると、今回の記事では曲げモーメント図の書き方について勉強していきましょう。 曲げモーメント図とは、材料に働く曲げモーメントを図に表したものです。 英語ではBMD(Bending Moment Diagram)と言います。 曲げモーメント図の書き方は、せん断力図の書き方を知っていると理解しやすくなります部材両端の変位を全体座標系から部材座標系 に座標変換を行う。 材端力より部材断面力を計算し、部材荷重が ある場合は、両端固定の断面力を加える。 部材中央の曲げモーメントを計算する。 剛性行列と両端の変位を掛け算して、材端力 を計算する。



梁の公式 1 せん断力と曲げモーメント コンサルhiroの構造解析入門講座



両端支持梁のせん断力計算問題 複数の集中荷重を受ける場合 建築学科のための材料力学
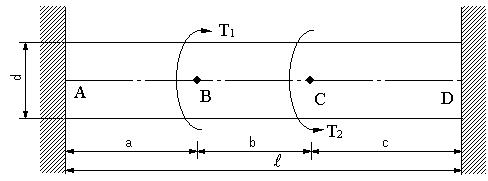
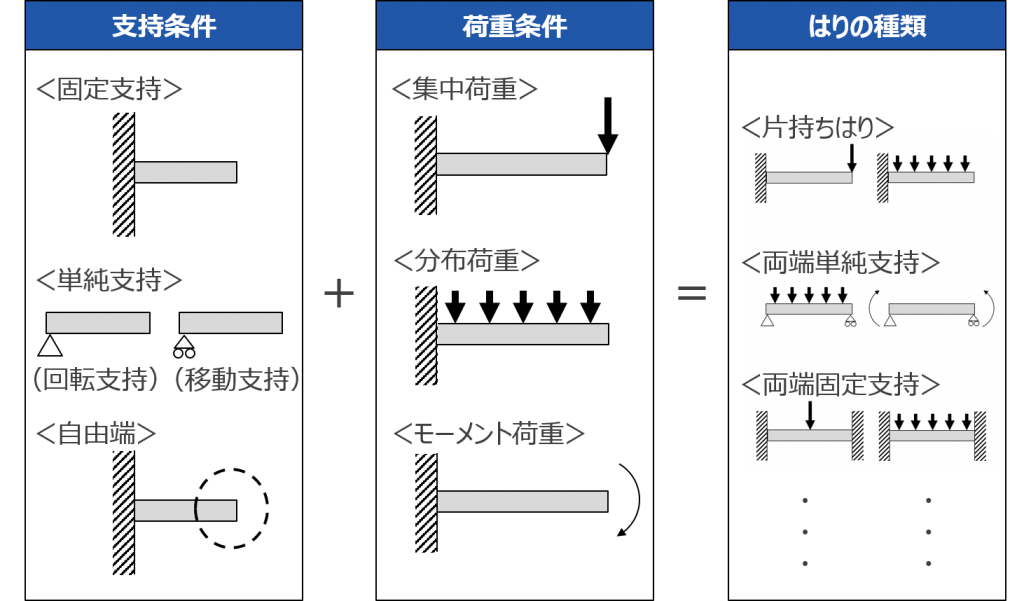
図のように両端が固定されている軸に、ねじりモーメントt1,t2が作用するとき、軸ab,bc,cdに作用するねじりモーメント、各軸のねじれ角、各軸に生ずるせん断応力を求める。剛性率g,断面二次極モーメントj,極断面係数z p,t 1 >t 2 とする。 解答例 問題223両端固定で部材角により 単位モーメント Ψ Ψ Ψ Ψ Ψ Ψ Ψ Ψ Ψ Ψ モーメント図・せん断力図 m0 求まった材端に 作用するモーメント 多層ラーメン 解を求める のは煩雑 d値法 教科書p52 長方形ラーメンが床の位置に水平力を受けたとき の応力を求める33 曲げを受ける部材の強さ 331 はりに作用する力 (1) はりの種類 ・片持はり(ばり) 一端が固定されているはり
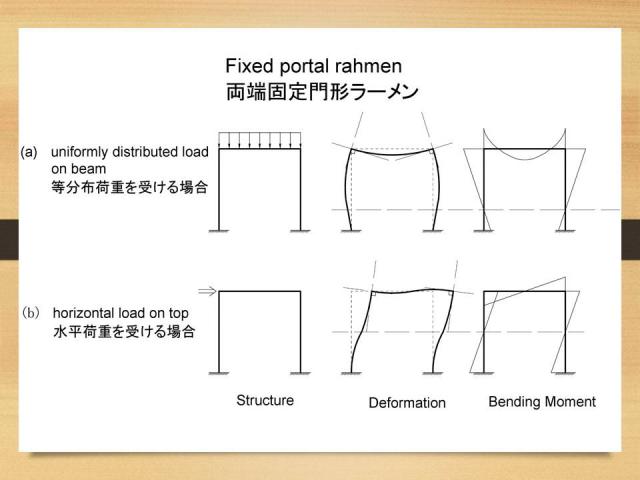



直観力学講座part2 両端固定門形ラーメンfixed Portal Rahmen 土木ウォッチング



今月のまめ知識 第10回 有効に 剛性 を出す組合せ Nic アルファマガジン Com
荷重・形状 条件 曲げモーメント m反力 r・せん断力 q・全荷重 w たわみ δ P l Rb a b w=p rb=p qb=-p mb=-pl pl3 δa= 3ei l Rb a b P1 P2 abrb=p1+p2 qb=-(p1+p2) w=p1+p2 mb=-(p1l+p2b) 2 δa= + 3ei p1l3 6ei p2b (3l-b) l Rb a b ab P w=p rb=pモーメント 荷重 せん断 力 モーメント 荷重 せん断 力 abの時 最大 xbの時 x固定法を使用するために、表の中で扱い易い数字とするためである。こ の強制変位である部材角を与えると、柱の両端に生じる材端モーメント 図27b 軸力図と反力・外力図 500 500



4 1 梁の境界値問題



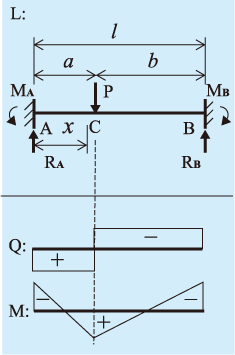
両端支持梁の支点反力を求める例題を紹介 建築学科のための材料力学
固定端モーメントの定義 両端固定とした時の、中間荷重により両端に生じ るモーメント cab, cba 中間荷重のある場合の基本式 b a ba a a b ab c ei m c ei m 2τ τ 2 2τ τ 2M:曲げモーメント図 W:全荷重 M:曲げモーメント R:反力 θ:回転角 Q:せん断力 δ:たわみ 両端固定 中心荷重 両端固定 偏芯荷重 両端固定 等分布荷重 kanpro 公式集-梁構造List42 集中せん断力や集中モーメントの作用 421 集中外力の作用と連続条件 ここまでは1径間の梁に分布外力や端外力が与えられた系を対象として, 静定・不静定を問わず一般的な梁の解法の基礎と特徴を説明してきた。




1級建築士試験 構造力学 分割モーメントと水平剛性の問題 1級建築士 ワンワンの建築世界



材料力学の問題です 両端固定ばりabが図6 15に示すように一部分に一様 Yahoo 知恵袋
マリンエンジニアのための材料力学入門講座(その2) Journal of the JIME Vol 44, No3(09) ―80― 日本マリンエンジニアリング学会誌 第44巻 第3号(09) 418 日本マリンエンジニアリング学会執筆要項 Journal of the JIME Vol00,No00(05) -2- 日本マリンエンジニアリング学会誌 第00 巻 第00 号 (05)I はじめに ドイツ人数学者のClebsch は,100 年前に「弾性体の理論」(Theorie der Elasticit¨at fester K¨orper) を著している.長い間,この本は,弾性理論一般についてとりわけ変位に ついて理解しやすい内容の本として好評であった.10 年に出版されたSaalschutz¨ の 「荷重を受ける棒」(Der belastete Stab固定モーメント法の考え方 連続梁ABC A C k B ab kbc P B kab k bc CA kab kbc P CB 両端固定梁AB + 固定解除 モーメント 分配モーメント MAB =kab(ψB) MBA =kab(2ψB ) MBC =kbc(2ψB ) MCB =kbc(ψB ) (a) 連続梁に作用するモーメント A C B MB (b) 連続梁の変形 A C B θB θB kab kbc




両端固定はりのせん断力と曲げモーメント 図のような固定はりのせん断力 曲 Okwave
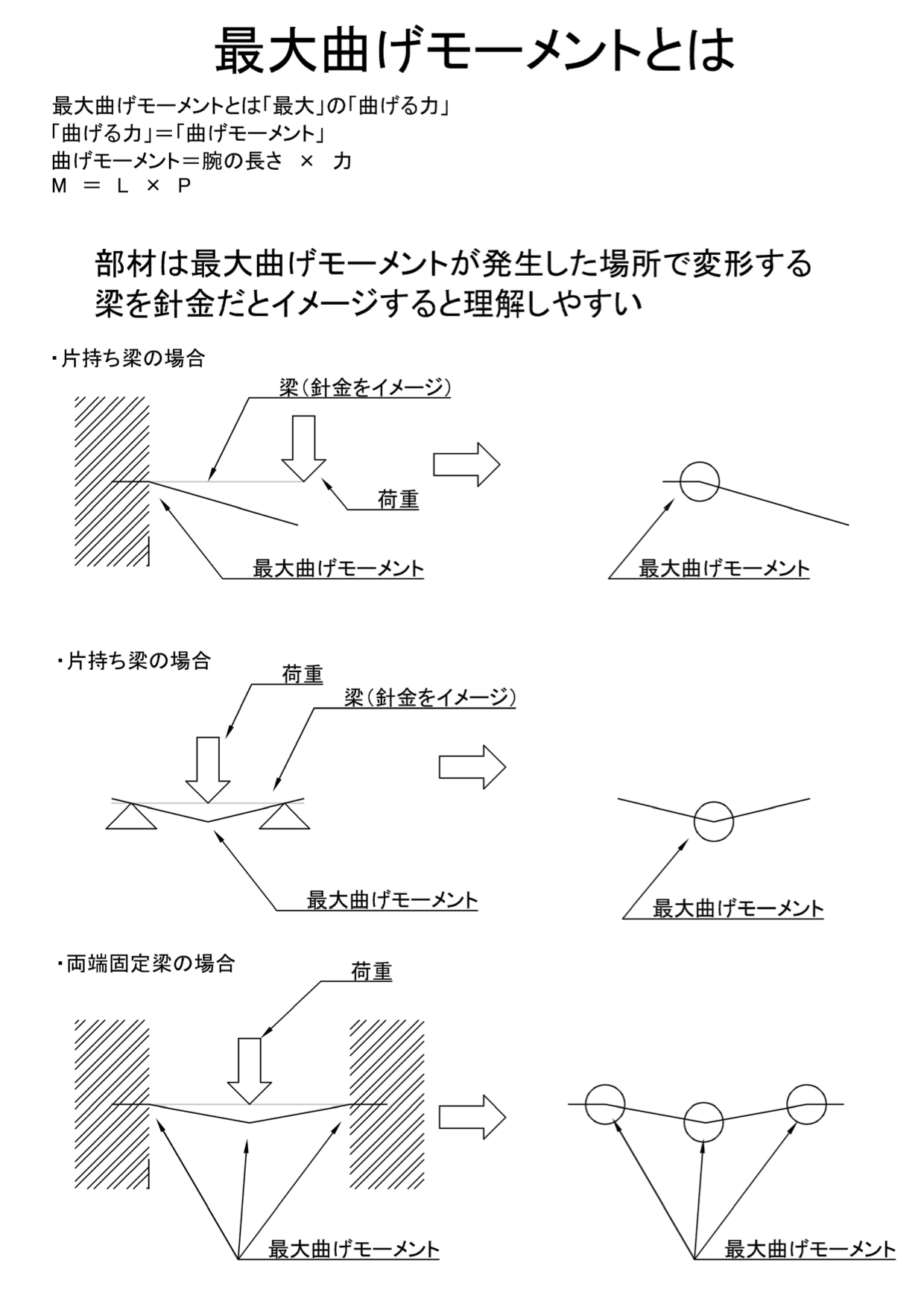



最大曲げモーメントとは 見える化に挑戦 機械卒でも土木の現場監督
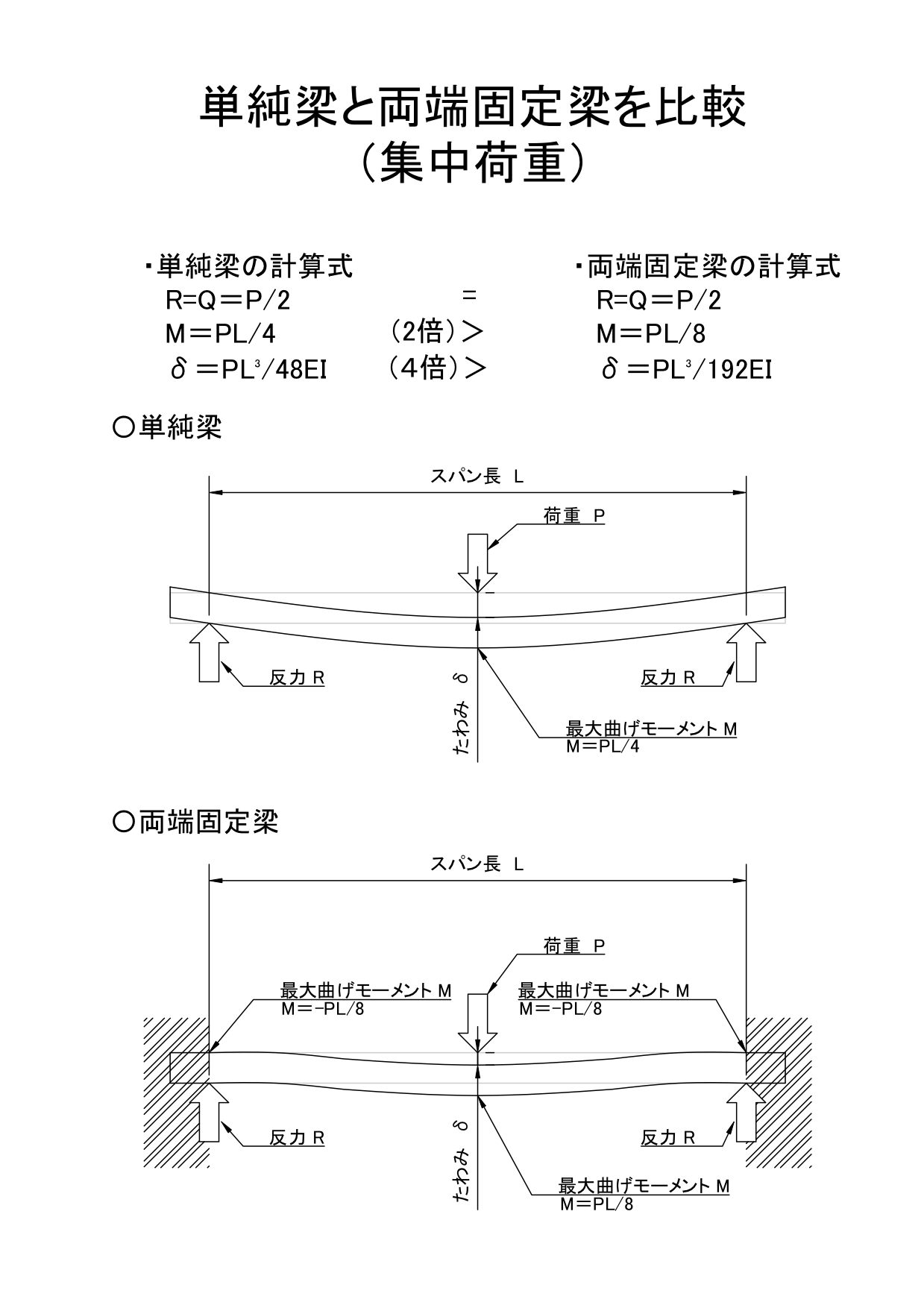
Cb 間では負ですね。したがって、sfd は図3 のようになります。qac = r1 はac 間に働くせん断力、 qcb = −r2(= r1 −p) はcb 間に働くせん断力になります。 0 r1 () r2 () a c b p 図3 sfd 学生先生!質問です。今の話だと、反力の正負を考えるとき、上向きを正としているように思いますが・・・?次に固定端からx の点の仮想断面に働くせん断力 F とモーメント M を求める。図 613は左端から仮想断面までの部分のFBDである。 図613 仮想断面を含む部分のFBD 力のつり合いから RAA qx F F R qx q l x0() (613) C点回りのモーメントのつり合いから 2 0 0単純梁と両端固定梁を比較単純梁の方が変位が大きい 最大せん断力については集中荷重・等分布荷重どちらも同じである。 荷重を負担するのが両端2箇所で同じであるため、同様の値となる。 最大曲げモーメントはどちらの荷重条件でも単純梁のほう



Ex 5



公式集 構造計算 両端固定梁 曲げモーメント せん断 反力 たわみ
両端の支点でのモーメント •両端の支点では、固定支点でなければ支点 モーメントは作用しない。 𝑀1=𝑀 =0 この2つの式と中間の支点に作用するk-2個の支 点モーメントを持ち数として3モーメントの式を




07 号 車体前部の組付構造 Astamuse



材料力学についての質問です 両端支持はりで任意の位置でのたわみの問 Yahoo 知恵袋



Ex364



たわみ角法の基本式 長さl 曲げ剛性eiのラーメンの一部材abが中間荷重を受けて 移動 変形したときの材端モーメントmab Mba 時計回りが は Ppt Download



曲げモーメント図の書き方 両端支持梁の場合はどうなる 建築学科のための材料力学




はりの強度計算 両端固定 等分布荷重 三角形 製品設計知識



両端固定梁のたわみ 応力 支持反力 集中荷重



第8章 構造解析法への適用
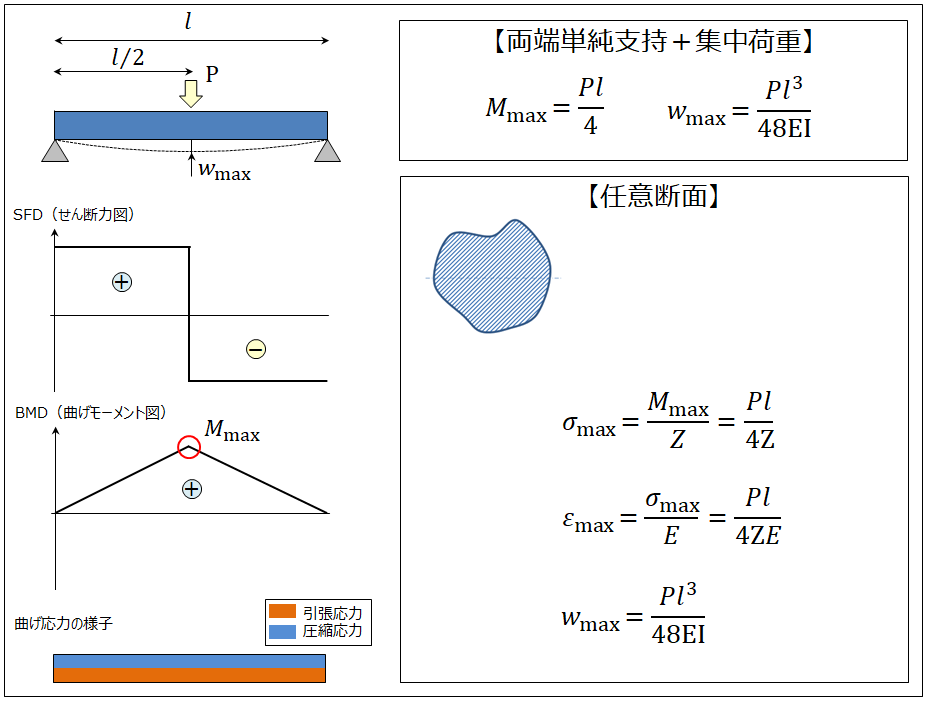



はりの強度計算 両端単純支持 集中荷重 任意断面 製品設計知識



単純梁の構造計算 せん断 剪断 曲げモーメント たわみ 撓み 計算 無料フリーソフトダウンロード
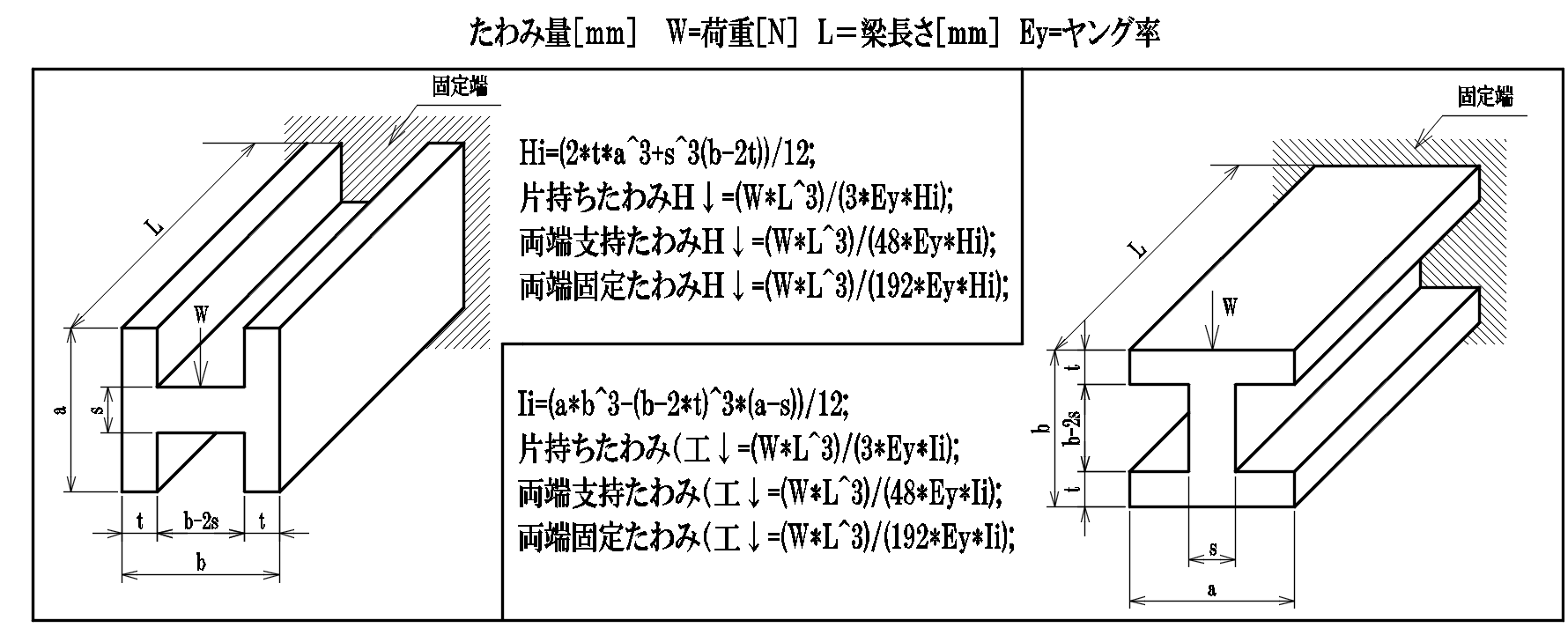



H鋼のたわみ比較 高精度計算サイト




はりのひずみの計算式 共和電業



両端固定はりのたわみ計算 はりのたわみ計算 オンライン



材料力学の典型的な問題



連続はり



やさしい実践 機械設計講座



小梁の設計 C M Qとは 構造設計memo



両端支持はりの最大曲げ応力は 1分でわかる求め方 公式



単純梁と両端固定梁を比較 単純梁の方が変位が大きい 機械卒でも土木の現場監督



はりの解析に定義した値 符号 座標軸の取り方等について




第6回 固定 と 支持 その大きな違い 日経クロステック Xtech



はりの話 前編
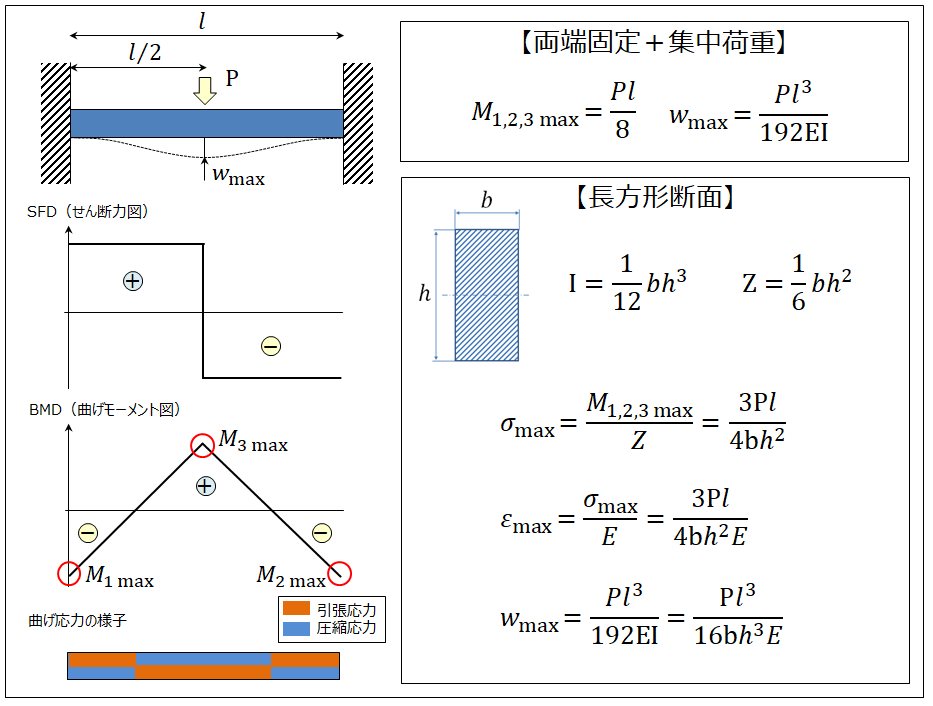



はりの強度計算 両端固定 集中荷重 長方形 製品設計知識



梁のたわみ量の計算について



1



はりの曲げモーメントせん断力解説



1




平成28年度 技術士一次試験 機械部門択一 5 両端を固定した丸棒のねじり角 古賀恭一郎の日記



Stage Tksc Jaxa Jp Taurus Member Miyazaki Old Lecture Strength Of Materials Ii 15 Pdf



構造計算 両端固定梁 切削 樹脂 プレス レーザー加工の特急試作なら日新産業株式会社



曲げモーメントの公式は 1分でわかる公式 導出 両端固定 単純梁 片持ち梁



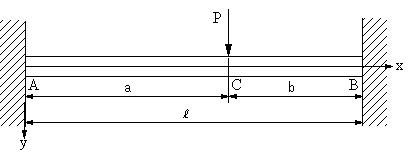
大学の材料力学の問題です下記に示す両端固定はりに集中荷重pが作用 Yahoo 知恵袋



たわみ角法の基本式 長さl 曲げ剛性eiのラーメンの一部材abが中間荷重を受けて 移動 変形したときの材端モーメントmab Mba 時計回りが は Ppt Download



曲げモーメントの公式は 1分でわかる公式 導出 両端固定 単純梁 片持ち梁



4 2 集中せん断力や集中モーメントの作用



はりの曲げモーメントせん断力解説



単純 梁 片 持ち 梁



Ex 5



1
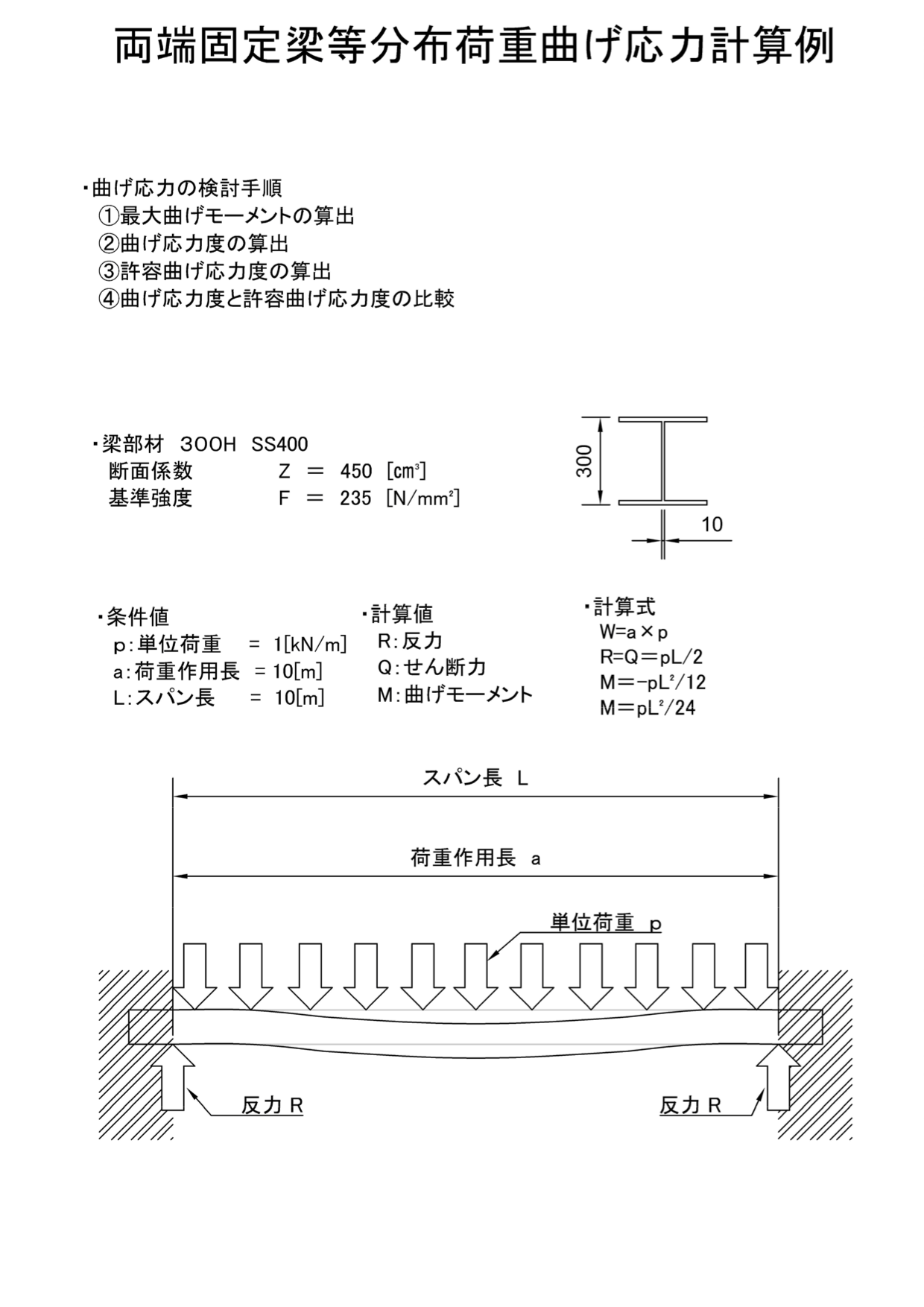



両端固定梁曲げ応力計算例 H300 等分布荷重 機械卒でも土木の現場監督



曲げモーメントの公式は 1分でわかる公式 導出 両端固定 単純梁 片持ち梁
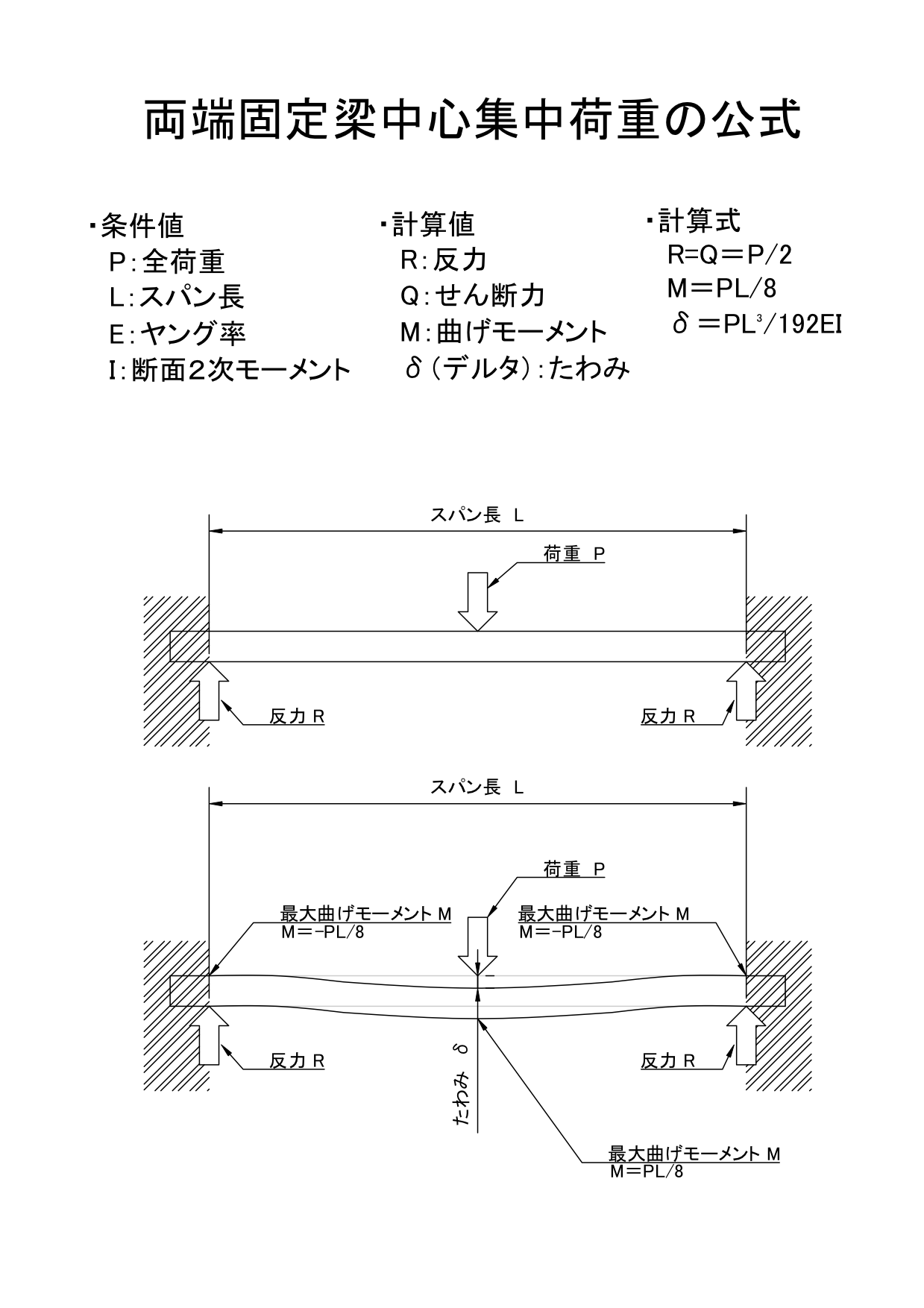



両端固定梁とは 梁の両端を接合 機械卒でも土木の現場監督



公式集 構造計算 両端固定梁 曲げモーメント せん断 反力 たわみ



梁 反力 曲げモーメント たわみ 曲げ応力 公式集 計算ツール ものづくりのススメ



はりの曲げモーメントせん断力解説




01 2813号 荷重支持構造 Astamuse
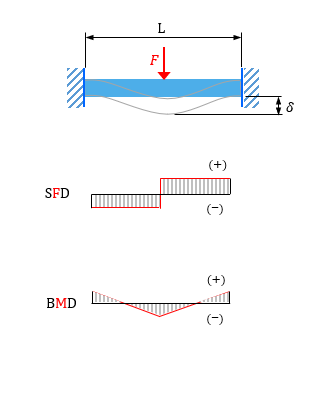



梁のたわみと応力計算ツール



Excelを使った数値計算ツールsuitexl



単純梁の構造計算 せん断 剪断 曲げモーメント たわみ 撓み 計算 無料フリーソフトダウンロード



固定端モーメントとは 1分でわかる意味 片持ち梁とc 両端固定梁




材料力学 ライブラリ Opeo 折川技術士事務所
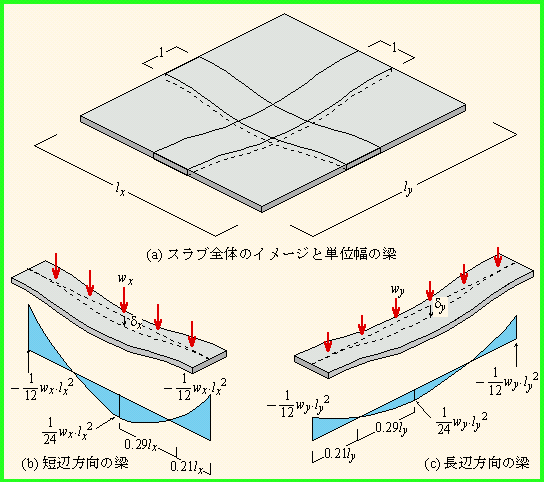



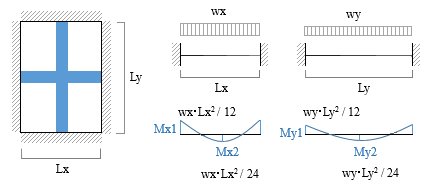
8 2 周辺固定スラブ



梁のたわみと応力計算ツール




ラーメンの曲げモーメント公式集 両脚固定矩形ラーメン 4 P3



両端支持梁の曲げモーメントの求め方は 計算方法について 建築学科のための材料力学




材料力学静定梁両端固定の最大たわみ 材料力学の静定梁の問題です 両端固定 Okwave



2点集中荷重が作用する両端固定梁の公式は 1分でわかる求め方 解き方 と計算




M Sudo S Room 特殊はりの曲げモーメントを計算する手法 両端固定
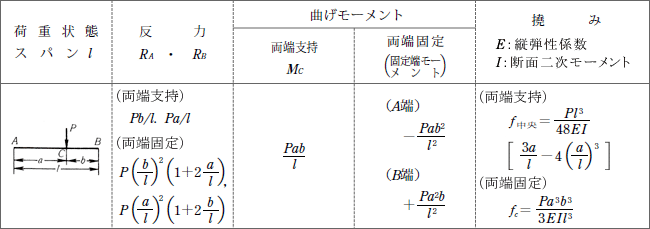



梁の反力 曲げモーメント及び撓み 9 P381



両端固定梁とは 1分でわかる意味 曲げモーメント たわみ 解き方



種々のはりのたわみ




梁の計算4 両端固定梁 集中荷重 1 Youtube



両端固定梁とは 1分でわかる意味 曲げモーメント たわみ 解き方



両端固定梁 等分布荷重



はりの話 前編



中間荷重の処理



Www Jp Omega Com Techref Pressure43 67 Pdf



はりの話 前編



電卓で構造計算 スラブ編



材料力学の問題です 下図のように両固定端の梁に等分布荷重がかかっていま Yahoo 知恵袋



2点集中荷重が作用する両端固定梁の公式は 1分でわかる求め方 解き方 と計算



プラスチック製品の強度設計基礎講座 第2回 基本的な強度計算の方法 Kabuku Connect カブクコネクト



構造計算 両端固定梁 切削 樹脂 プレス レーザー加工の特急試作なら日新産業株式会社




M Sudo S Room 両端固定の3連モーメント法の計算



種々のはりのたわみ
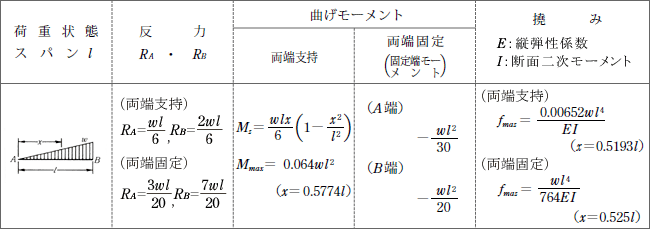



梁の反力 曲げモーメント及び撓み 18 P381




10 号 ロードセル Astamuse



今月のまめ知識 第36回 アルミフレームのつなぎ方 Nic アルファマガジン Com



はりの曲げモーメントせん断力解説



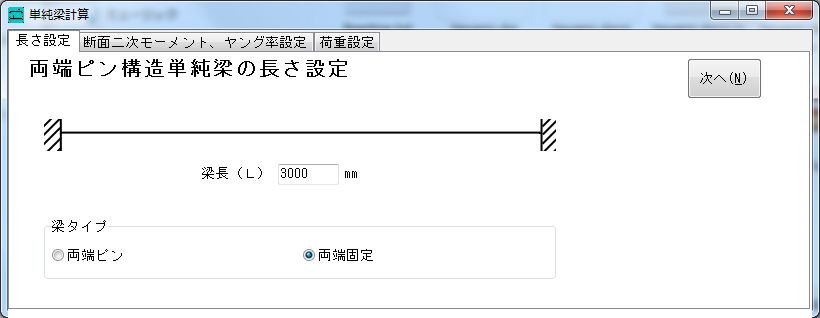
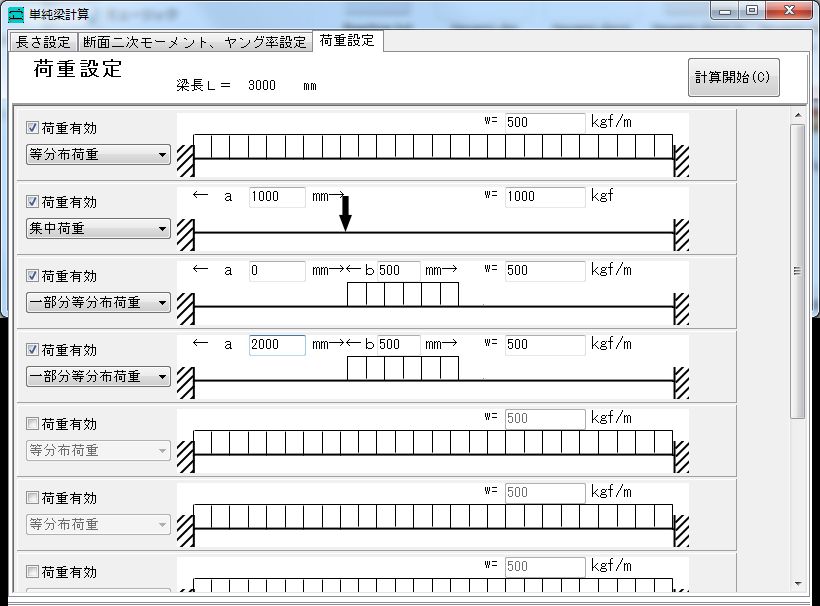
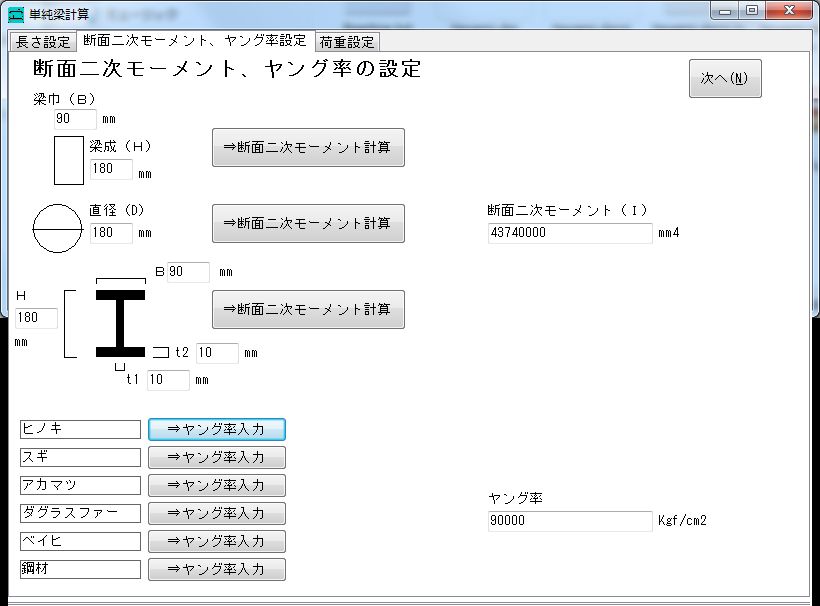
梁柱計算名人の両端固定梁計算画面



Www Jp Omega Com Techref Pressure43 67 Pdf



公式集 構造計算 両端固定梁 曲げモーメント せん断 反力 たわみ



第8章 構造解析法への適用
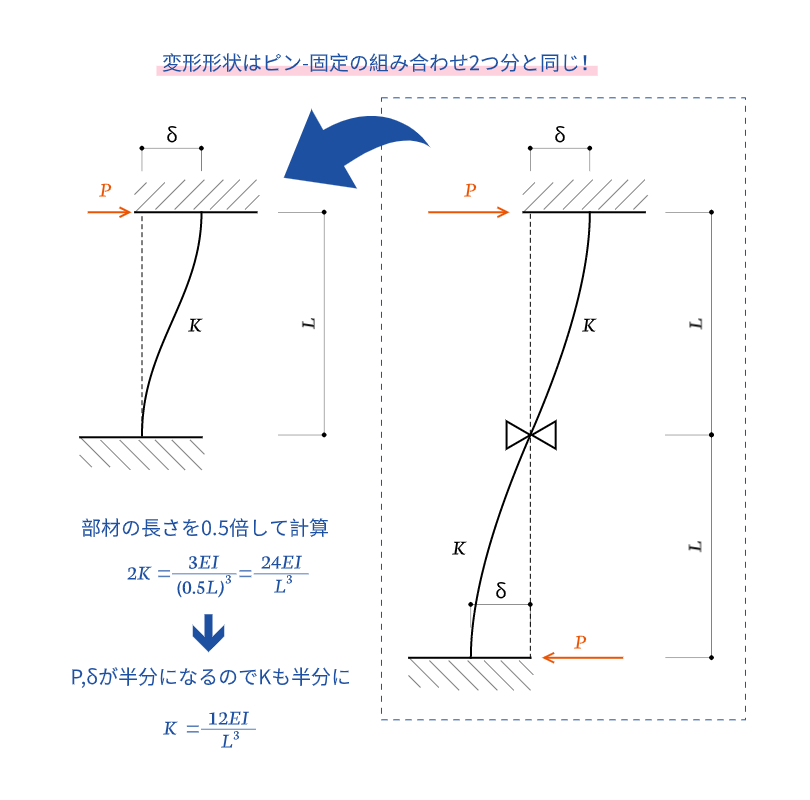



構造力学 水平剛性の問題の解き方を解説 ゆるっと建築ライフ



公式集 構造計算 両端固定梁 曲げモーメント せん断 反力 たわみ
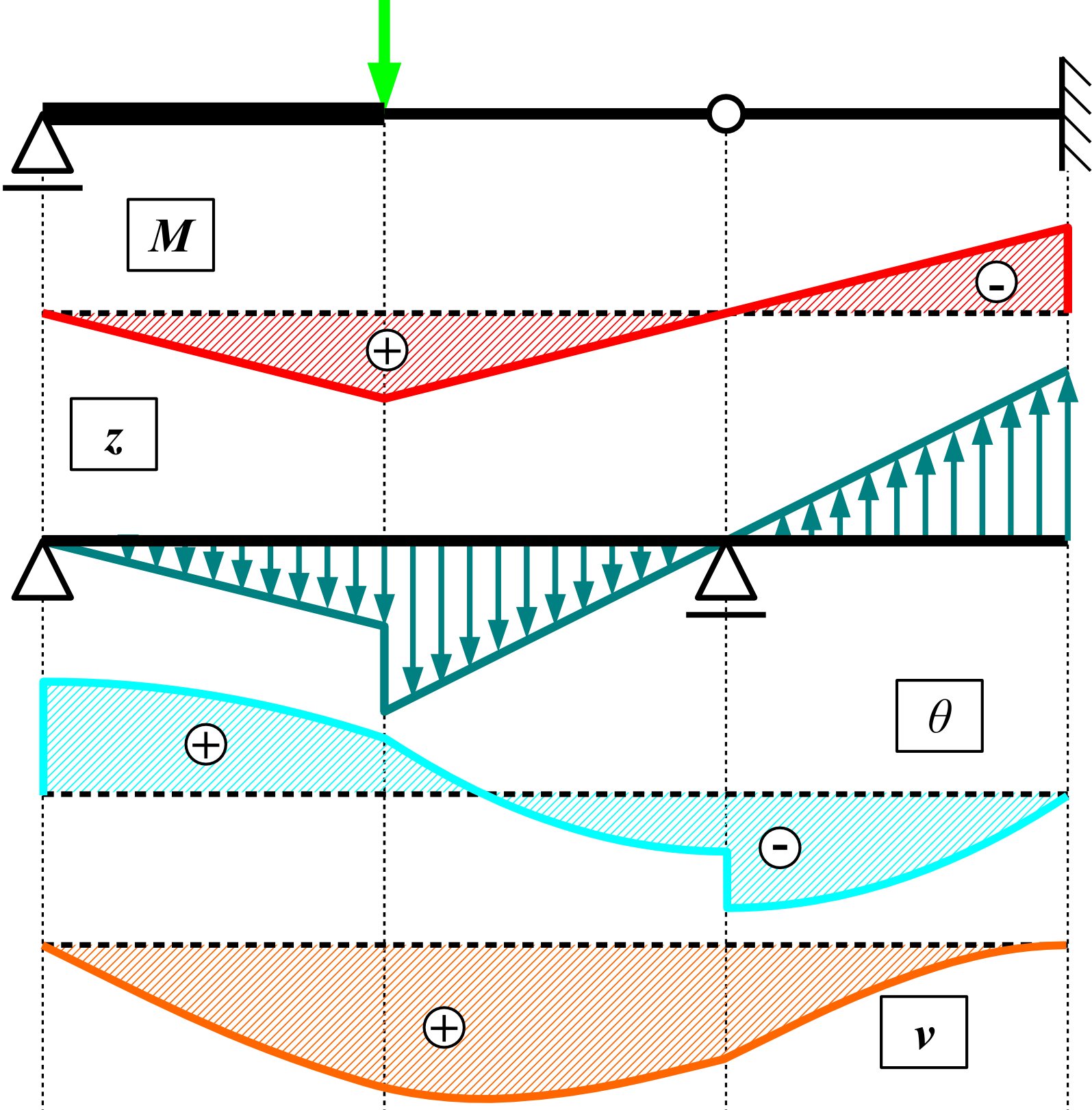



モールの定理 Wikipedia



0 件のコメント:
コメントを投稿